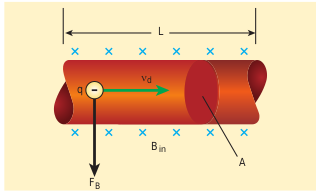
When a current carrying conductor is placed in a magnetic field, the force experienced by the conductor is equal to the sum of Lorentz forces on the individual charge carriers in the conductor. Consider a small segment of conductor of length (dl), with cross-sectional area (A) and current (I) as shown in Figure 3.51. The free electrons drift opposite to the direction of the current. So the relation between current (I) and the magnitude of drift velocity (v_d) (Refer Unit 2) is

$$ I = neAv_d , (3.65) $$

If the conductor is kept in a magnetic field (\vec{B}), then the average force experienced by the charge (electron) in the conductor is

$$ \vec{F_e} = -e \vec{v_d} \times \vec{B} $$

If (n) is the number of free electrons present in unit volume, then

$$ n = \frac{N}{V} $$

where (N) is the number of free electrons in the small element of volume (V = Adl).

Hence Lorentz force on the elementary section of length (dl) is the product of the number of the electrons ((N = nAdl)) and the force acting on each electron.

$$ \vec{F} = -e n Adl \vec{v_d} \times \vec{B} $$

The current element in the conductor is (Idl = enAdl v_d). Therefore the force on the small elemental section of the current-carrying conductor is

$$ d\vec{F} = I , dl , \vec{B} , (3.66) $$

$$ d\vec{q} $$

$$ \vec{F_B} $$

$$ \vec{B}_{\text{in}} $$

$$ \vec{L} $$

$$ \vec{A} $$

(-)

EXAMPLE 3.23

Suppose a cyclotron is operated to accelerate protons with a magnetic field of strength (1 , \text{T}). Calculate the frequency in which the electric field between two Dees could be reversed.

Solution

Magnetic field (B = 1 , \text{T}), mass of the proton (m_p = 1.67 \times 10^{-27} , \text{kg}), charge of the proton (q = 1.6 \times 10^{-19} , \text{C}).

$$ f = \frac{q B}{2\pi m_p} = \frac{1.6 \times 10^{-19} \times 1}{2 \times \pi \times 1.67 \times 10^{-27}} , \text{Hz} $$

$$ f \approx 3 , \text{MHz} $$

Thus, the force on a straight current-carrying conductor of length (l) placed in a uniform magnetic field is

$$ \vec{F} = I , \vec{l} \times \vec{B} , (3.67) $$

In magnitude,

$$ F = BIl \sin \theta_{\text{total}} $$

(a) If the conductor is placed along the direction of the magnetic field, then the angle ( \theta ) is (0^\circ ). Hence, the force experienced by the conductor is zero.

(b) If the conductor is placed perpendicular to the magnetic field, then the angle ( \theta = 90^\circ ). Hence, the force experienced by the conductor is maximum, which is ( F_{\text{total}} = BIl ).

Fleming’s left hand rule When a current-carrying conductor is placed in a magnetic field, the direction of the force experienced by it is given by Fleming’s Left Hand Rule (FLHR) as shown in Figure 3.52.

Figure 3.52 Fleming’s Left Hand Rule (FLHR)

$$ \text{Force} \quad \quad \text{Magnet} $$

$$ \text{Current} $$

Stretch out forefinger, the middle finger, and the thumb of the left hand such that they are in three mutually perpendicular directions. If the forefinger points in the direction of the magnetic field, the middle finger in the direction of the electric current, then the thumb will point in the direction of the force experienced by the conductor.

EXAMPLE 3.24

A metallic rod of linear density is (0.25 , \text{kg m}^{-1}) is lying horizontally on a smooth inclined plane which makes an angle of (45^\circ) with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of strength (0.25 , \text{T}) is acting on it in the vertical direction. Calculate the electric current flowing in the rod to keep it stationary.

$$ \vec{mg} \sin 45^\circ $$

$$ \vec{B} $$

$$ 45^\circ $$

$$ \vec{I} $$

$$ \vec{B}_{\text{in}} $$

$$ \vec{T} $$

Solution

The linear density of the rod, i.e., mass per unit length of the rod is (0.25 , \text{kg m}^{-1})

$$ \Rightarrow \lambda = \frac{m}{l} = 0.25 , \text{kg m}^{-1} $$

Let (I) be the current flowing in the metallic rod. The direction of the electric current is into the plane of the paper. The direction of magnetic force (\vec{IBl}) is given by Fleming’s left-hand rule.

$$ \vec{mg} \sin 45^\circ $$

$$ \vec{B} $$

$$ 45^\circ $$

$$ 45^\circ $$

$$ \vec{BI}_l \cos 45^\circ $$

$$ \vec{BI}_l $$

$$ \vec{I} $$

$$ \vec{B}_{\text{in}} $$

For equilibrium of the rod,

$$ \vec{mg} , \vec{IBl} \sin 45^\circ \cos 45^\circ = 0 $$

$$ \Rightarrow I , B , m , l , g , \tan 45^\circ = \frac{0.25 \times 1 \times 9.8}{2} , \text{A} $$

$$ \Rightarrow I = \frac{0.25 \times 1 \times 9.8}{2} , \text{A} $$

$$ \Rightarrow I = 0.25 , \text{A} $$

So, we need to supply a current of 0.25 A to keep the metallic rod stationary.