Cyclotron (Figure 3.49) is a device used to accelerate charged particles to gain large kinetic energy. It is also called a high energy accelerator and was invented by Lawrence and Livingston in 1934.

Principle

When a charged particle moves perpendicular to the magnetic field, it experiences magnetic Lorentz force.

$$ v_0 = \frac{E}{B} $$

Construction

The schematic diagram of a cyclotron is shown in Figure 3.50. The particles move between two semi-circular metal containers called Dees (hollow D-shaped objects). Dees are enclosed in an evacuated chamber and are kept in a region with a uniform magnetic field controlled by an electromagnet. The direction of the magnetic field is normal to the plane of the Dees. The two Dees are kept separated with a gap, and the source (S) (which ejects the particle to be accelerated) is placed at the center in the gap between the Dees. Dees are connected to a high-frequency alternating potential difference.

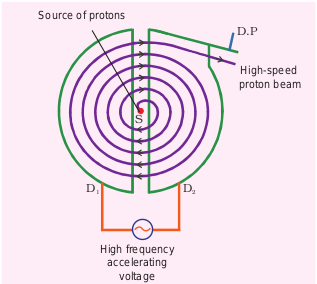
Working

Let us assume that the ion ejected from the source (S) is positively charged. As soon as the ion is ejected, it is accelerated towards a Dee (say, Dee – 1) which has a negative potential at that time. Since the magnetic field is normal to the plane of the Dees, the ion moves in a circular path. After one semi-circular path inside Dee-1, the ion reaches the gap between Dees. At this time, the polarities of the Dees are reversed, so the ion is now accelerated towards Dee-2 with greater velocity. For this circular motion, the centripetal force on the charged particle (q) is provided by the Lorentz force.

$$ \frac{m r v^2}{r} = q B v $$

$$ v \propto \frac{r}{\sqrt{r}} $$

From the equation (3.63), the increase in velocity increases the radius of the circular path. This process continues, and hence the particle moves in a spiral path of increasing radius. Once it reaches near the edge, it is taken out with the help of a deflector plate and allowed to hit the target (T).

The important condition in cyclotron operation is that the frequency (f) at which the positive ion circulates in the magnetic field must be equal to the constant frequency of the electrical oscillator (f_{\text{osc}}). This is called the resonance condition.

$$ f = \frac{q B}{2\pi m} $$

The time period of oscillation is

$$ T = \frac{2\pi m}{q B} $$

The kinetic energy of the charged particle is

$$ KE = \frac{1}{2} m q B r^2 $$

Limitations of cyclotron (a) The speed of the ion is limited. (b) Electrons cannot be accelerated. (c) Uncharged particles cannot be accelerated.

Note

EXAMPLE 3.23

Suppose a cyclotron is operated to accelerate protons with a magnetic field of strength 1 T. Calculate the frequency in which the electric field between two Dees could be reversed.

Solution

Magnetic field (B = 1 , \text{T}), mass of the proton (m_p = 1.67 \times 10^{-27} , \text{kg}), charge of the proton (q = 1.6 \times 10^{-19} , \text{C}).

$$ f = \frac{q B}{2\pi m_p} = \frac{1.6 \times 10^{-19} \times 1}{2 \times \pi \times 1.67 \times 10^{-27}} , \text{Hz} $$

$$ f \approx 3 , \text{MHz} $$