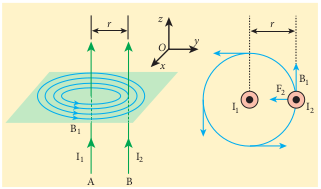
Let two long straight parallel current carrying conductors separated by a distance (r) be kept in an air medium as shown in Figure 3.53. Let (I_1) and (I_2) be the electric currents passing through the conductors A and B in the same direction (i.e., along (z)-direction) respectively. The net magnetic field at a distance (r) due to current (I_1) in conductor A is

$$ \vec{B_1} = \frac{\mu I_1}{2\pi r} \hat{i} $$

$$ B_1 $$

$$ B_1 $$

$$ I_1 $$

$$ I_1 $$

$$ A $$

$$ B $$

$$ \vec{r} $$

$$ I_2 $$

$$ I_2 $$

$$ F_2 $$

$$ \hat{z} $$

$$ \hat{x} $$

$$ \hat{y} $$

$$ O $$

From the thumb rule, the direction of the magnetic field is perpendicular to the plane of the paper and inwards (arrow into the page (\otimes)), i.e., along the negative (\hat{i}) direction.

Let us consider a small elemental length (dl) in conductor B at which the magnetic field (\vec{B_1}) is present. From equation 3.66, Lorentz force on the element (dl) of conductor B is

$$ d\vec{F} = I dl \vec{B_1} = I dl \frac{\mu I_1}{2\pi r} \hat{j} $$

Therefore the force on (dl) of the wire B is directed towards the conductor A. So the element of length (dl) in B is attracted towards the conductor A. Hence the force per unit length of the conductor B due to current in the conductor A is

$$ \vec{F_l} = -I_1I_2\frac{\mu}{2\pi r} \hat{j} $$

Similarly, the net magnetic induction due to current (I_2) (in conductor B) at a distance (r) in the elemental length (dl) of conductor A is

$$ \vec{B_2} = \frac{\mu I_2}{2\pi r} \hat{i} $$

From the thumb rule, the direction of the magnetic field is perpendicular to the plane of the paper and outwards (arrow out of the page (\epsilon)), i.e., along the positive (\hat{i}) direction. Hence, the magnetic force acting on element (dl) of the conductor A is

$$ d\vec{F} = I dl \vec{B_2} = I dl \frac{\mu I_2}{2\pi r} \hat{j} $$

Therefore the force on (dl) of conductor A is directed towards the conductor B. So the length (dl) is attracted towards the conductor B as shown in Figure (3.54).

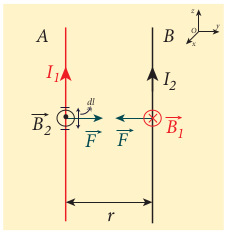
The force acting per unit length of the conductor A due to the current in conductor B is

$$ \vec{F_l} = I_1I_2\frac{\mu}{2\pi r} \hat{j} $$

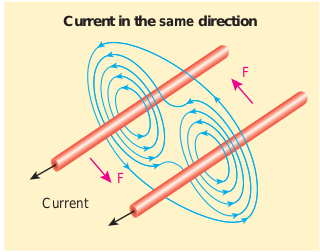
Thus, the force between two parallel current carrying conductors is attractive if they carry current in the same direction (Figure 3.55).

$$ \text{Current} \quad \quad \vec{F} \quad \quad \vec{F} $$

Current in the same direction

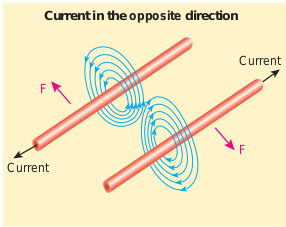
The force between two parallel current carrying conductors is repulsive if they carry current in opposite directions (Figure 3.56).

$$ \text{Current} \quad \quad \text{Current} \quad \quad \vec{F} \quad \quad \vec{F} $$

Definition of ampere: One ampere is defined as that constant current which, when passed through each of the two infinitely long parallel straight conductors kept side by side parallelly at a distance of one meter apart in air or vacuum, causes each conductor to experience a force of (2 \times 10^{-7}) newton per meter length of conductor.