REFRACTION AT SINGLE SPHERICAL SURFACE
We have so far studied only the refraction at plane surface. The refraction can also take place at spherical surface between two transparent media. The laws of refraction hold good at every point on the spherical surface. The normal at the point of incidence is perpendicular drawn to the tangent plane of the spherical surface at that point. Therefore, the normal always passes through its center of curvature. The study of refraction at single spherical surface paves way to the understanding of thin lenses which consist of two refracting surfaces.
The following assumptions are made while considering refraction at spherical surfaces.
(i) The incident light is assumed to be monochromatic (single colour)
(ii) The incident light is very close to the principal axis (paraxial rays).
The sign conventions are similar to that of the spherical mirrors.
Equation for refraction at single spherical surface
Let us consider two transparent media with refractive indices _n_1 and _n_2 which are separated by a spherical surface as shown in Figure 6.31. Let C be the centre of curvature of the spherical surface. Let a point object O be in the medium _n_1. The line OC is the principal axis that cuts the spherical surface at the pole P. As the rays considered are paraxial rays, the perpendicular dropped from the point of incidence to the principal axis is very close to the pole (or) passes through the pole itself.
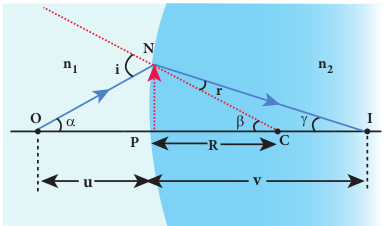
Light from O falls on the refracting surface at N. The normal drawn to the refracting surface at the point of incidence passes through the centre of curvature C. As _n_2>_n_1, light in the denser medium deviates towards the normal and meets the principal axis at I where the image is formed.
Snell’s law in product form for the refraction at the point N can be written from equation (6.19),
\(n_{1} \sin i=n_{2} \sin r\)As the angles are small, sine of the angle could be approximated to the angle itself.
\(n_{1} i=n_{2} r\)Let the angles be,
\(\angle N O P=\alpha, \angle N C P=\beta, \angle N I P=\gamma\)From the right angle triangles \(\triangle N O P\) , \(\triangle N C P\) and \(\triangle N I P\) ,
\(\tan \alpha=\frac{P N}{P O} ; \quad \tan \beta=\frac{P N}{P C} ; \quad \tan \gamma=\frac{P N}{P I}\)As these angles are small, tan of the angle could be approximated to the angle itself.
\(\alpha=\frac{P N}{P O} ; \beta=\frac{P N}{P C} ; \gamma=\frac{P N}{P I}\)For the triangle, \(\triangle O N C\) ,
\(i=\alpha+\beta\)For the triangle, \(\triangle I N C\) ,
\(\beta=r+\gamma\) (or) \(r=\beta-\gamma\)
Substituting for i and r from equations (6.53) and (6.54) in the equation (6.51).
\(n_{1}(\alpha+\beta)=n_{2}(\beta-\gamma)\)After rearranging,
\(n_{1} \alpha+n_{2} \gamma=\left(n_{2}-n_{1}\right) \beta\)Substituting for \(\alpha, \beta\) and \(\gamma\) from equation (6.52),
\(n_{1}\left(\frac{P N}{P O}\right)+n_{2}\left(\frac{P N}{P I}\right)=\left(n_{2}-n_{1}\right)\left(\frac{P N}{P C}\right)\)Further simplifying by cancelling PN,
\(\frac{n_{1}}{P O}+\frac{n_{2}}{P I}=\frac{n_{2}-n_{1}}{P C}\)Following sign conventions, \(P O=-u\) , \(P I=+v\) and \(P C=+R\) in equation (6.58),
\(\frac{n_{1}}{-u}+\frac{n_{2}}{v}=\frac{\left(n_{2}-n_{1}\right)}{R}\)After rearranging, finally we get,
\(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{R}\)Equation (6.56) gives the relation among the object distance u, image distance v, refractive indices of the two media \(\left(n_{1}\right.\) and \(\left.n_{2}\right)\) and the radius of curvature $R$ of the spherical surface. It holds good for any spherical surface as sign conventions are applied.
If the first medium is air, then \(n_{1}=1\) and for the second medium \(n_{2}=n\) , then the equation is reduced to,
\(\frac{n}{v}-\frac{1}{u}=\frac{(n-1)}{R}\)EXAMPLE 6.12
Locate the image of the point object $O$ in the situation shown. The point $C$ denotes the centre of curvature of the separating surface.
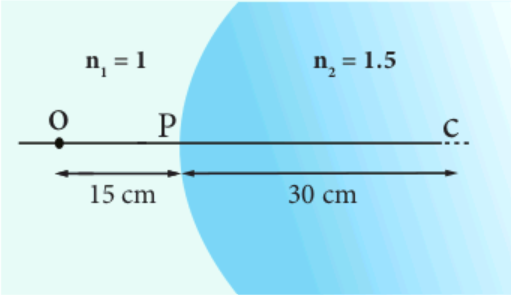
Solution Given, \(u=-15 \mathrm{~cm}, R=30 \mathrm{~cm}, n_{1}=1\) and \(n_{2}=1.5\)
Equation for single spherical surface is,
\(\frac{n_{2}}{v}-\frac{n_{1}}{u}=\frac{\left(n_{2}-n_{1}\right)}{R}\)Substituting the values,
\(\frac{1.5}{v}-\frac{1}{-15}=\frac{(1.5-1)}{30} ; \quad \frac{1.5}{v}+\frac{1}{15}=\frac{(0.5)}{30}\) \(\frac{1.5}{v}+\frac{1}{15}=\frac{1}{60} ; \quad \frac{1.5}{v}=\frac{1}{60}-\frac{1}{15} ;\) \(\frac{1.5}{v}=\frac{1-4}{60}=\frac{-3}{60} ;=-\frac{1}{20} ; v=-30 \mathrm{~cm}\)The image is a virtual image formed $30 \mathrm{~cm}$ to the left of the spherical surface.