Consider a charged particle of charge ( q ) having mass ( m ) entering into a region of uniform magnetic field ( \mathbf{B} ) with velocity ( \mathbf{v} ) such that velocity is perpendicular to the magnetic field. As soon as the particle enters into the field, Lorentz force acts on it in a direction perpendicular to both magnetic field ( \mathbf{B} ) and velocity ( \mathbf{v} ). As a result, the charged particle moves in a circular orbit as shown in Figure 3.45. The Lorentz force on the charged particle is given by

$$ \mathbf{F} = q \mathbf{B} \times \mathbf{v} $$

Since Lorentz force alone acts on the particle, the magnitude of the net force on the particle is

$$ F = \frac{qBv}{m} $$

This Lorentz force acts as centripetal force for the particle causing it to execute circular motion. Therefore,

$$ \frac{qvB}{m} = \frac{v^2}{r} $$

The radius of the circular path is

$$ r = \frac{mv}{qB} \quad \text{(3.57)} $$

where ( p = mv ) is the magnitude of the linear momentum of the particle. Let ( T ) be the time taken by the particle to finish one complete circular motion, then

$$ T = \frac{2\pi}{v} $$

Hence substituting (3.57) in (3.58), we get

$$ T = \frac{m}{qB} \frac{1}{2\pi} \quad \text{(3.59)} $$

Equation (3.59) is called the cyclotron period. The reciprocal of time period is the frequency ( f ), which is

$$ f = \frac{1}{T} = \frac{qB}{2\pi m} \quad \text{(3.60)} $$

In terms of angular frequency ( \omega ),

$$ \omega = \frac{\pi}{2} \frac{q}{m} B \quad \text{(3.61)} $$

Equations (3.60) and (3.61) are called as cyclotron frequency or gyro-frequency.

From equations (3.59), (3.60), and (3.61), we infer that time period and frequency depend only on charge-to-mass ratio (specific charge) but not on velocity or the radius of the circular path.

If a charged particle moves in a region of uniform magnetic field such that its velocity is not perpendicular to the magnetic field, then the velocity of the particle is split up into two components; one component is parallel to the field while the other component perpendicular to the field. The component of velocity parallel to the field remains unchanged, and the component perpendicular to the field keeps changing due to Lorentz force. Hence the path of the particle is not a circle; it is a helix around the field lines.

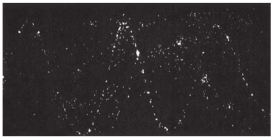
For example, the helical path of an electron when it moves in a magnetic field is shown in Figure 3.47. Inside the particle detector called a cloud chamber, the path is made visible by the condensation of water droplets.

EXAMPLE 3.19

An electron moving perpendicular to a uniform magnetic field 0.500 T undergoes circular motion of radius 2.50 mm. What is the speed of the electron?

Solution

Charge of an electron ( q = -1.60 \times 10^{-19} ) C ⇒ ( q = -e )

Magnitude of magnetic field ( B = 0.500 ) T

Mass of the electron, ( m = 9.11 \times 10^{-31} ) kg

Radius of the orbit, ( r = 2.50 ) mm = ( 2.50 \times 10^{-3} ) m

Speed of the electron,

$$ v = \frac{q rB}{m} = \frac{1.60 \times 10^{-19} \times 2.50 \times 10^{-3} \times 0.500}{9.11 \times 10^{-31}} $$

$$ v = 2.195 \times 10^8 , \text{m/s} $$

EXAMPLE 3.20

A proton moves in a uniform magnetic field of strength 0.500 T magnetic field is directed along the x-axis. At initial time, ( t = 0 ), the proton has velocity ( \mathbf{v} = (1.95 \times 10^5 \mathbf{i} + 2.00 \times 10^5 \mathbf{j} + 5.00 \times 10^5 \mathbf{k}) ) m/s. Find

(a) At initial time, what is the acceleration of the proton.

(b) Is the path circular or helical? If helical, calculate the radius of helical trajectory and also calculate the pitch of the helix (Note: Pitch of the helix is