When an electric charge $$ q $$ is moving with velocity $$ \vec{v} $$ in the magnetic field $$ \vec{B} $$, it experiences a force, called magnetic force $$ \vec{F}_m $$. After careful experiments, Lorentz deduced the force experienced by a moving charge in the magnetic field:

$$ \vec{F}_m = q (\vec{v} \times \vec{B}) \quad (3.55) $$

In magnitude, $$ F_m = qv\sin(\theta) $$ (3.56)

The equations (3.55) and (3.56) imply:

1. $$ \vec{F}_m $$ is directly proportional to the magnetic field $$ \vec{B} $$
2. $$ \vec{F}_m $$ is directly proportional to the velocity $$ \vec{v} $$ of the moving charge
3. $$ \vec{F}_m $$ is directly proportional to the sine of the angle between the velocity and magnetic field
4. $$ \vec{F}_m $$ is directly proportional to the magnitude of the charge $$ q $$
5. The direction of $$ \vec{F}_m $$ is always perpendicular to $$ \vec{v} $$ and $$ \vec{B} $$ as $$ \vec{F}_m $$ is the cross product of $$ \vec{v} $$ and $$ \vec{B} $$.

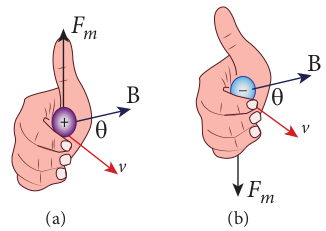
6. The direction of $$ \vec{F}_m $$ on a negative charge is opposite to the direction of $$ \vec{F}_m $$ on a positive charge provided other factors are identical, as shown in Figure 3.44 (b).
7. If the velocity $$ \vec{v} $$ of the charge $$ q $$ is along the magnetic field $$ \vec{B} $$, then $$ \vec{F}_m $$ is zero.

Definition of tesla: The strength of the magnetic field is one tesla if a unit charge moving in it with unit velocity experiences unit force.

$$ 1 , \text{T} = 1 , \text{Ns/C m} = 1 , \text{N/A m} = 1 , \text{N A}^{-1} m^{-1} $$

EXAMPLE 3.17

A particle of charge $$ q $$ moves with velocity $$ \vec{v} $$ along the positive $$ y $$-direction in a magnetic field $$ \vec{B} $$. Compute the Lorentz force experienced by the particle: (a) when the magnetic field is along the positive $$ y $$-direction, (b) when the magnetic field points in the positive $$ z $$-direction, (c) when the magnetic field is in the zy-plane and making an angle $$ \theta $$ with the velocity of the particle. Mark the direction of the magnetic force in each case.

Solution

Velocity of the particle is $$ \vec{v} = \hat{j} $$.

(a) Magnetic field is along positive $$ y $$-direction, which implies $$ \vec{B} = \hat{j} $$. From Lorentz force, $$ \vec{F}_m = q (\vec{v} \times \vec{B}) = \vec{0} $$. So, no force acts on the particle when it moves along the direction of the magnetic field.

(b) Since the magnetic field points in positive $$ z $$-direction, which implies $$ \vec{B} = \hat{k} $$. From Lorentz force, $$ \vec{F}_m = q (\vec{v} \times \vec{B}) = qv \hat{i} $$. Therefore, the magnitude of the Lorentz force is $$ qvB $$ and the direction is along the positive $$ x $$-direction.

(c) Magnetic field is in the zy-plane and making an angle $$ \theta $$ with the velocity of the particle, which implies $$ \vec{B} = \hat{j}\cos(\theta) + \hat{k}\sin(\theta) $$. From Lorentz force, $$ \vec{F}_m = q (\vec{v} \times \vec{B}) = qvB\sin(\theta) \hat{i} $$. Therefore, the magnitude of the Lorentz force is $$ qvB\sin(\theta) $$ and the direction is along the positive $$ x $$-direction.

EXAMPLE 3.18

Compute the work done and power delivered by the Lorentz force on the particle of charge $$ q $$ moving with velocity $$ \vec{v} $$. Calculate the angle between the Lorentz force and velocity of the charged particle and also interpret the result.

Solution

For a charged particle moving in a magnetic field, $$ \vec{F}_m = q (\vec{v} \times \vec{B}) $$.

The work done by the magnetic field is $$ W = \int \vec{F}_m \cdot d\vec{r} $$, which is zero since $$ \vec{F}_m $$ and $$ d\vec{r} $$ are perpendicular to each other.

$$ \frac{dW}{dt} = \vec{F}_m \cdot \vec{v} = 0 $$

Since $$ \vec{F}_m $$ and $$ \vec{v} $$ are perpendicular to each other, the angle between them is $$ 90^\circ $$. Thus, the Lorentz force changes the direction of the velocity but not the magnitude of the velocity. Hence, the Lorentz force does no work and also does not alter the kinetic energy of the particle.