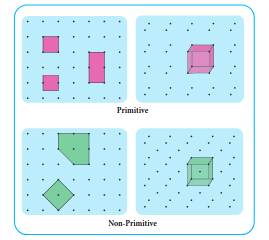
Primitive and non-primitive unit cell
There are two types of unit cells: primitive and non-primitive. A unit cell that contains only one type of lattice point is called a primitive unit cell, which is made up from the lattice points at each of the corners.
In case of non-primitive unit cells, there are additional lattice points, either on a face of the unit cell or with in the unit cell.
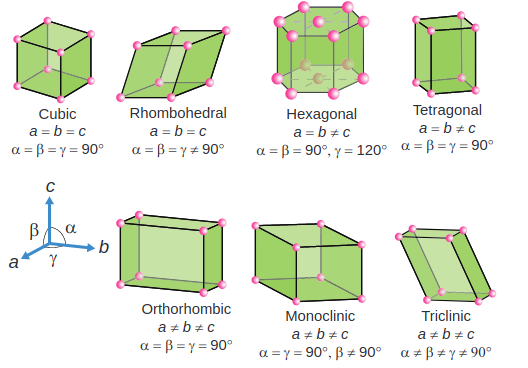
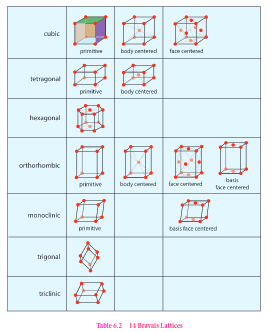
There are seven primitive crystal systems; cubic, tetragonal, orthorhombic, hexagonal, monoclinic, triclinic and rhombohedral. They differ in the arrangement of their crystallographic axes and angles. Corresponding to the above seven, Bravis defined 14 possible crystal systems as shown in the figure.
Number of atomes in cubic cell
Primitive (or) simple cubic unit cell.(SC)
In the simple cubic unit cell, each corner is occupied by an identical atoms or ions or molecules. And they touch along the edges of the cube, do not touch diagonally. The coordination number of each atom is 6.
Each atom in the corner of the cubic
unit cell is shared by 8 neighboring unit
cells and therefore atoms `per unit cell is
equal to N 8
c , where Nc is the number of
atoms at the corners.
∴ Number of atoms in a SC unit cell∴ =
Body centered cubic unit cell. (BCC)
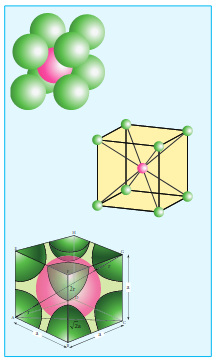
In a body centered cubic unit cell, each corner is occupied by an identical particle and in addition to that one atom occupies the body centre. Those atoms which occupy the corners do not touch each other, however they all touch the one that occupies the body centre. Hence, each atom is surrounded by eight nearest neighbours and coordination number is 8. An atom present at the body centre belongs to only to a particular unit cell i.e unshared by other unit cell.
∴ Number of atoms in a bcc unit cell =
Face centered cubic unit cell.(FCC)
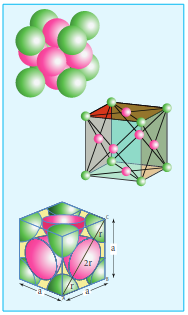
∴ Number of atoms in a fcc unitcell =
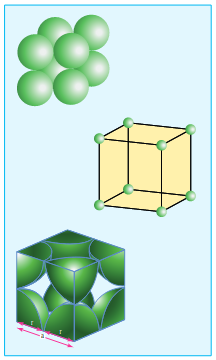
Drawing the crystal lattice on paper is not an easy task. The constituents in a unit cell touch each other and form a three dimensional network. This can be simplified by drawing crystal structure with the help of small circles (spheres) corresponding constituent particles and connecting neighbouring particles using a straight line as shown in the figure.
Calculations involving unit cell dimensions:
X-Ray diffraction analysis is the most powerful tool for the determination of crystal structure. The inter planar distance (d) between two successive planes of atoms can be calculated using the following equation form the X-Ray diffraction data 2dsin = nθ λ
The above equation is known as Bragg’s equation.
Where
λ is the wavelength of X-ray used for diffraction.
θ is the angle of diffraction
n is the order of diffraction
By knowing the values of θ λ, and n we can calculate the value of d.
d = n 2sin
Using these values the edge length of the unit cell can be calculated.
Calculation of density:
Using the edge length of a unit cell, we can calculate the density ρ( ) of the crystal by considering a cubic unit cell as follows.
Density of the unit cell ρ = mass of the unit cell
volume of the unit cell
…(1)
mass of the unit cell= total number of atoms belongs to that unit cell
mass of one atom
mass of one atom molar mass gmol Avagadro number (mol
Substitute (3) in (2)
mass of the unit cell= n M NA
× …(4)
For a cubic unit cell, all the edge lengths are equal i.e , a=b=c volume of the unit cell = a a a = a3× × …(5)
∴ Density of the unit cell ρ n M a N3
A
= …(6)
Equation (6) contains four variables namely ρ , n , M and a . If any three variables are known, the fourth one can be calculated.
Example 2
Barium has a body centered cubic unit cell with a length of 508pm along an edge. What is the density of barium in g cm-3?
Solution:
ρ n M a N3
In this case,
n=2 ; M=137.3 gmol-1 ; a = 508pm= 5.08X10-8cm
ρ 2 atoms 137.3 g mol 5.08 cm 6.023 a
3= × ×( ) ×
−10 108 23 toms mol
2 137.3 5.08 6.023
( ) = ×
( ) × × × ρ
10 1024 23 m
g cm
Evaluate yourself -1
1. An element has a face centered cubic unit cell with a length of 352.4 pm along an edge. The density of the element is 8.9 gcm-3. How many atoms are present in 100 g of an element?
2. Determine the density of CsCl which crystallizes in a bcc type structure with an edge length 412.1 pm.
3. A face centered cubic solid of an element (atomic mass 60) has a cube edge of 4 A 0
. Calculate its density.