COMPONENTS OF A VECTOR
In the Cartesian coordinate system, any vector \(\vec{A}\) can be resolved into three components along \(x, y\) and \(z\) directions. This is shown in Figure 2.20.
Consider a 3-dimensional coordinate system. With respect to this, a vector can be written in component form as
\(\vec{A}=A_{x} \hat{i}+A_{y} \hat{j}+A_{z} \hat{k}\)
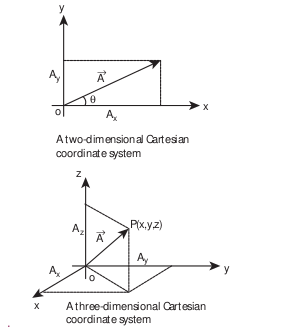
Figure 2.20 Components of a vector in 2 dimensions and 3 dimensions
Here \(\vec{A}_{x}\) is the \(x\) -component of \(\vec{A}\) , \(A_{y}\) is the \(y\) -component of \(\vec{A}\) , and \(A_{z}\) is the \(z\) -component of \(\vec{A}\) .
In a 2-dimensional Cartesian coordinate system (which is shown in Figure 2.20) the vector \(\vec{A}\) is given by
\(\vec{A}=A_{x} \hat{i}+A_{y} \hat{j}\)If \(\vec{A}\) makes an angle \(\theta\) with \(\mathrm{x}\) axis, and \(A_{x}\) and \(A_{y}\) are the components of \(\vec{A}\) along \(x\) -axis and \(y\) -axis respectively, then as shown in Figure 2.21,
\(A_{x}=A \cos \theta, A_{y}=A \sin \theta\)where ’ \(A\) ’ is the magnitude (length) of the vector \(\vec{A}\) , \(A=\sqrt{A_{x}^{2}+A_{y}^{2}}\)
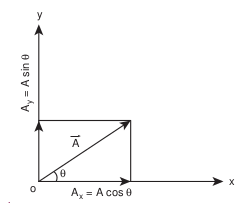
Figure 2.21 Resolution of a vector
EXAMPLE 2.3
What are the unit vectors along the negative x–direction, negative y–direction, and negative z– direction?
Solution
The unit vectors along the negative directions can be shown as in the following figure.
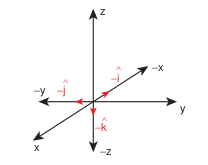
Then we have: The unit vector along the negative \(\mathrm{x}\) direction is \(-\hat{i} \) . The unit vector along the negative \(y \) direction is \(-\hat{j} \) . The unit vector along the negative \(\mathrm{z}\) direction is \(-\hat{k} \) .
Vector addition using components
In the previous section we have learnt about addition and subtraction of two vectors using geometric methods. But once we choose a coordinate system, the addition and subtraction of vectors becomes much easier to perform.
The two vectors \( \vec{A} \) and \(\vec{B}\) in a Cartesian coordinate system can be expressed as
\(\begin{aligned} \vec{A} & =A_{x} \hat{i}+A_{y} \hat{j}+A_{z} \hat{k} \\ \vec{B} & =B_{x} \hat{i}+B_{y} \hat{j}+B_{z} \hat{k} \end{aligned}\)Then the addition of two vectors is equivalent to adding their corresponding x, y and z components.
\(\vec{A}+\vec{B}=\left(A_{x}+B_{x}\right) \hat{i}+\left(A_{y}+B_{y}\right) \hat{j}+\left(A_{z}+B_{z}\right) \hat{k}\)Similarly, the subtraction of two vectors is equivalent to subtracting the corresponding \( x, y and z \) components.
\(\vec{A}-\vec{B}=\left(A_{x}-B_{x}\right) \hat{i}+\left(A_{y}-B_{y}\right) \hat{j}+\left(A_{z}-B_{z}\right) \hat{k}\)The above rules form an analytical way of adding and subtracting two vectors.
EXAMPLE 2.4
Two vectors \(\vec{A}\) and \( \vec{B}\) are given in the component form as \( \vec{A}=5 \hat{i}+7 \hat{j}-4 \hat{k}\) and \( \vec{B}=6 \hat{i}+3 \hat{j}+2 \hat{k}\) . Find \( \vec{A}+\vec{B}\) and \( \vec{A}-\vec{B}\) .
Solution
\(\begin{aligned} \vec{A}+\vec{B} & =(5 \hat{i}+7 \hat{j}-4 \hat{k})+(6 \hat{i}+3 \hat{j}+2 \hat{k}) \\ & =11 \hat{i}+10 \hat{j}-2 \hat{k} \\ \vec{B}+\vec{A} & =(6 \hat{i}+3 \hat{j}+2 \hat{k})+(5 \hat{i}+7 \hat{j}-4 \hat{k}) \\ & =(6+5) \hat{i}+(3+7) \hat{j}+(2-4) \hat{k} \\ & =11 \hat{i}+10 \hat{j}-2 \hat{k} \\ \vec{A}-\vec{B} & =(5 \hat{i}+7 \hat{j}-4 \hat{k})-(6 \hat{i}+3 \hat{j}+2 \hat{k}) \\ & =-\hat{i}+4 \hat{j}-6 \hat{k} \\ \vec{B}-\vec{A} & =\hat{i}-4 \hat{j}+6 \hat{k} \end{aligned}\)Note that the vectors \(\vec{A}+\vec{B}\) and \(\vec{B}+\vec{A}\) are same and the vectors \(\vec{A}-\vec{B}\) and \(\vec{B}-\vec{A}\) are opposite to each other.
Note The addition of two vectors using components depends on the choice of the coordinate system. But the geometric way of adding and subtracting two vectors is independent of the coordinate system used