We have just learnt that the rate of change of concentration of the reactant is directly proportional to that of concentration of the reactant. For a general reaction,

A →products

The rate law is

Rate = -d[A]/dt=k [A]^x Where k is the rate constant, and x is the order of the reaction. The above equation is a differential equation, -d[A]/dt , so it gives the

rate at any instant. However, using the above expression, we cannot answer questions such as how long will it take for a specific concentration of A to be used up in the reaction? What will be the concentration of

reactant after a time ‘ t ’?. To answer such questions, we need the integrated form of the above rate law which contains time as a variable.

A reaction whose rate depends on the reactant concentration raised to the first power is called a first order reaction. Let us consider the following first order reaction,

A →prosuct Rate law can be expressed as

Rate = k [A]¹

Where, k is the first order rate constant. -d[A]/dt=k[A]¹ ⇒ = -d[A]/[A]= k dt …(1)

Integrate the above equation between the limits of time t = 0 and time equal to t, while the concentration varies from the initial concentration [A₀ ] to [A] at the later time.

∫^[A] _[A0] -d[A₀]/[A]=k∫^tdt

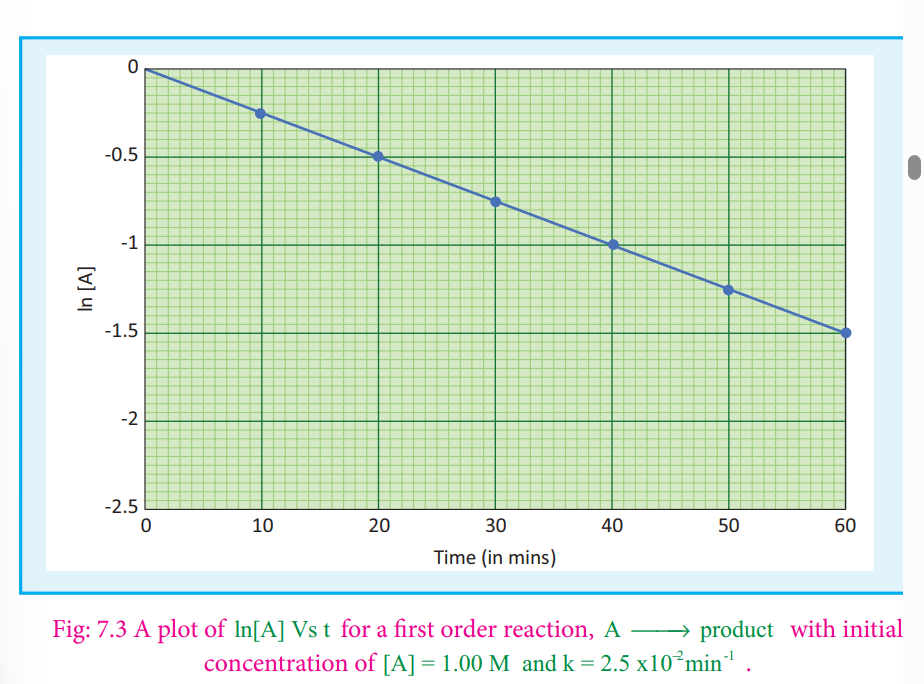
ln([A₀]/[A]) = kt …(2)

This equation is in natural logarithm. To convert it into usual logarithm with base 10, we have to multiply the term by 2.303.

2.303 log [A₀]/[A] = kt

Equation (2) can be written in the form y = mx + c as below

⇒y = c + mx

If we follow the reaction by measuring the concentration of the reactants at regular time interval‘t’, a plot of ln[A] against ‘t’ yields a straight line with a negative slope.From this, the rate constant is calculated.

Examples for the first order reaction

(i) Decomposition of dinitrogen pentoxide

N₂O₅(g)—> 2NO _2(g) + 1/2 O₂(g).

(ii) Decomposition of sulphurylchloride; SO₂Cl₂(l)—> SO₂(g)+ Cl₂(g).

(iii) Decomposition of the H₂O₂ in aqueous solution; H₂O₂(aq)—> H₂O(l)+1/2 O₂(g).

(iv) Isomerisation of cyclopropane to propene.

Pseudo first order reaction: Kinetic study of a higher order reaction is difficult to follow, for example, in a study of a second

order reaction involving two different reactants; the simultaneous measurement of change in the concentration of both the reactants is very difficult. To overcome such difficulties, A second order reaction can be altered to a first order reaction by taking one of the reactant in large excess, such reaction is called pseudo first order reaction. Let us consider the acid hydrolysis of an ester,

$\ce{CH3COOHCH3(aq)+H2O(l)->[{H+}] CH3COOH(aq)+CH3OH}$

Rate = k [CH₃COOCH₃] [H₂O]

If the reaction is carried out with the large excess of water, there is no significant change in the concentration of water during hydrolysis. i.e.,concentration of water remains almost a constant.

Now, we can define k[H₂ O] = k’; Therefore the above rate equation becomes

Rate = k’[CH₃COOCH₃]

Thus it follows first order kinetics.

A reaction in which the rate is independent of the concentration of the reactant over a

wide range of concentrations is called as zero order reactions. Such reactions are rare. Let us consider the following hypothetical zero order reaction.

A →product

The rate law can be written as,

Rate = k [A]⁰

−d[A]/ dt

=k (1)

∴ =([A]⁰=1)

⇒ − d[A] = k dt

Integrate the above equation between the limits of [A ] 0 at zero time and [A] at some later

time ’t',

− ∫d[A] = k ∫dt

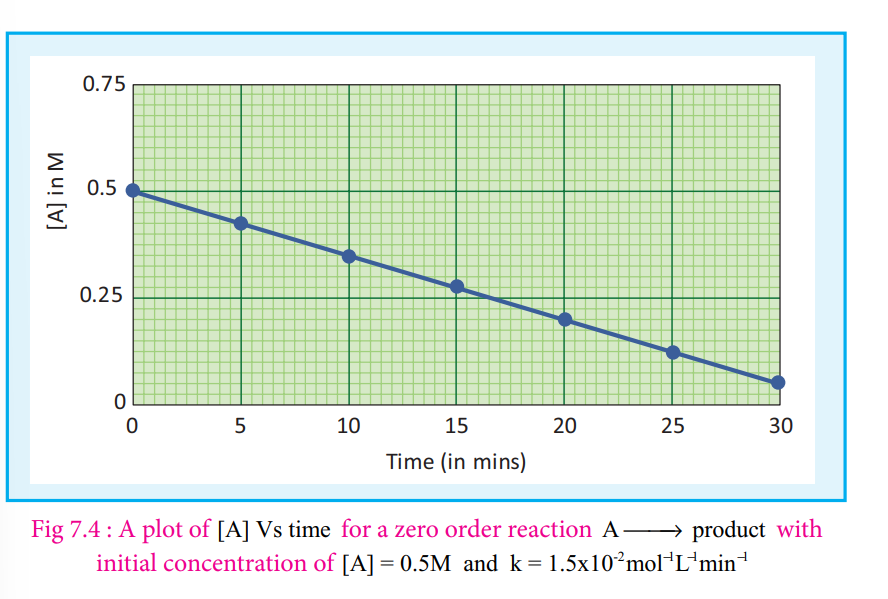
k=[A₀]-[A]/t

Equation (2) is in the form of a straight line y = mx + c

Ie., [A]=[A]/t ⇒ y = c + mx

A plot of [A] Vs time gives a straight line with a slope of −k and y - intercept of [A₀ ].

Examples for a zero order reaction: 1. Photochemical reaction between H2 and I2

$\ce{H2(g)+Cl2(g) ->[{hv}] 2HCL(g)}$

2. Decomposition of N2O on hot platinum surface

N₂O(g) ⇀↽N₂(g)+1/2O₂(g)

3. Iodination of acetone in acid medium is

zero order with respect to iodine.

$\ce{CH3COCH3+l2(g) ->[{h+}] ICH2COCH3+HI}$

Rate = k [CH₃COCH₃] [H⁺]

General rate equation for a nth order reaction involving one reactant [A].

A →product

Rate law − =d[A]/dt=k[A]ⁿ

Consider the case in which n≠1,

integration of above equation between [A₀] and [A] at time t = 0 and t = t

respectively gives 1/[A]^n-1 - 1/[A]^n-1 =(n-1)kt