Accuracy and Precision

Let us say, you know your true height is exactly 5′9″. You first measure your height with a yardstick and get the value 5′0″. Your measurement is hence not accurate. Now you measure your height with a laser yardstick and get 5′9″ as the value. Now your measurement is accurate. The true value is also called theoretical value. The level of accuracy required for each application varies greatly. Highly accurate data can be very difficult to produce and compile. For example, if you consistently measure your height as 5′0″ with a yard stick, your measurements are precise. The level of precision required for different applications vary to a great extent. Engineering projects such as road and utility construction require very precise information measured to the millimeter or one-tenth of an inch.

If a measurement is precise, that does not necessarily mean that it is accurate. However, if the measurement is consistently accurate, it is also precise.

For example, if the temperature outside a building is 40oC as measured by a weather thermometer and if the real outside

temperature is 40oC, the thermometer is accurate. If the thermometer consistently registers this exact temperature in a row, the thermometer is precise.

Consider another example. Let the temperature of a refrigerator repeatedly measured by a thermometer be given as 10.4oC, 10.2oC, 10.3oC, 10.1oC, 10.2oC, 10.1oC, 10.1oC, 10.1oC. However, if the real temperature inside the refrigerator is 9oC, we say that the thermometer is not accurate (it is almost one degree off the true value), but since all the measured values are close to 10oC, hence it is precise.

A visual example:

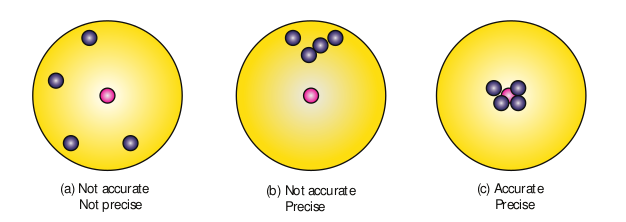
Target shooting is an example which explains the difference between accuracy and precision. In Figure 1.9 (a), the shots are focused so as to reach the bull’s eye (midpoint), but the arrows have reached only around this point. Hence the shots are not accurate and also not precise.

In Figure 1.9 (b), all the shots are close to each other but not at the central point. Hence the shots are said to be precise but not accurate. In Figure 1.9 (c), the shots are closer and also at the central point. Hence the shots are both precise and accurate.

A numerical example The true value of a certain length is nearly 5.678 cm. In one experiment, using a measuring instrument of resolution 0.1 cm, the measured value is found to be 5.5 cm. In another experiment using a measuring instrument of greater resolution, say 0.01 cm, the length is found to be 5.38 cm. We find that the first measurement is more accurate as it is closer to the true value, but it has lesser precision. On the contrary, the second measurement is less accurate, but it is more precise.