LAMI’S THEOREM

If a system of three concurrent and coplanar forces is in equilibrium, then Lami’s theorem states that the magnitude of each force of the system is proportional to sine of the angle between the other two forces. The constant of proportionality is same for all three forces.

Let us consider three coplanar and concurrent forces    F F F 1 2 3 , and which act at a common point O as shown in Figure 3.20. If the point is at equilibrium, then according to Lami’s theorem

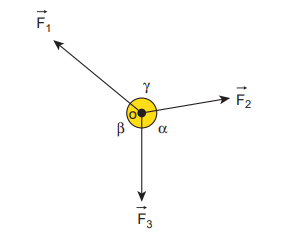
Figure 3.20 Three coplanar and concurrent forces    F F F 1 2 3 , and acting at O

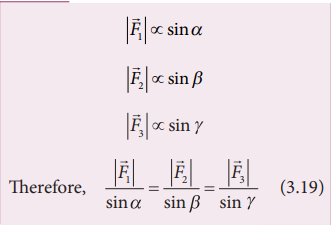
Lami’s theorem is useful to analyse the forces acting on objects which are in static equilibrium.

Application of Lami’s Theorem

EXAMPLE 3.14

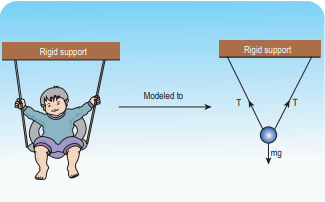
A baby is playing in a swing which is hanging with the help of two identical chains is at rest. Identify the forces acting on the baby. Apply Lami’s theorem and find out the tension acting on the chain.

Solution

The baby and the chains are modeled as a particle hung by two strings as shown in the figure. There are three forces acting on the baby.

i) Downward gravitational force along negative y direction (mg)

ii) Tension (T) along the two strings

These three forces are coplanar as well as concurrent as shown in the following figure.

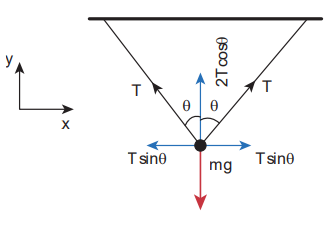
By using Lami’s theorem

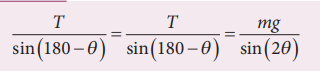
Since sin(180-θ) = sin θ and sin (2θ) = 2 sinθ cosθ

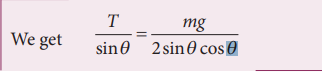
From this, the tension on each string is T mg  2cos .

Note

When   0 , the strings are vertical and the tension on each string is T mg = 2