DYNAMICS OF CIRCULAR MOTION

In the previous sections we have studied how to analyse linear motion using Newton’s laws. It is also important to know how to apply Newton’s laws to circular motion, since circular motion is one of the very common types of motion that we come across in our daily life. A particle can be in linear motion with or without any external force. But when circular motion occurs there must necessarily be some force acting on the object. There is no Newton’s first law for circular motion. In other words without a force, circular motion cannot occur in nature. A force can change the velocity of a particle in three different ways.

1. The magnitude of the velocity can be changed without changing the direction of the velocity. In this case the particle will move in the same direction but with acceleration.

Examples

Particle falling down vertically, bike moving in a straight road with acceleration.

2. The direction of motion alone can be changed without changing the magnitude (speed). If this happens continuously then we call it ‘uniform circular motion’.

3. Both the direction and magnitude (speed) of velocity can be changed. If this happens non circular motion occurs. For example oscillation of a swing or simple pendulum, elliptical motion of planets around the Sun.

In this section we will deal with uniform circular motion and non-uniform circular motion.

If a particle is in uniform circular motion, there must be centripetal acceleration towards the centre of the circle. If there is acceleration then there must be some force acting on it with respect to an inertial frame. This force is called centripetal force.

As we have seen in chapter 2, the centripetal acceleration of a particle in the circular motion is given by a v r = 2 and it acts towards centre of the circle. According to Newton’s second law, the centripetal force is given by

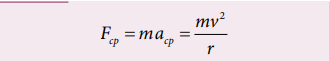
The word Centripetal force means centre seeking force.

In vector notation

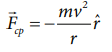
For uniform circular motion 2 ˆ cp F m    r r 

The direction –rˆ points towards the centre of the circle which is the direction of centripetal force as shown in Figure 3.38.

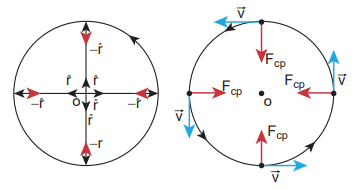
Figure 3.38 Centripetal force

It should be noted that ‘centripetal force’ is not other forces like gravitational force or spring force. It can be said as ‘force towards centre’. The origin of the centripetal force can be gravitational force, tension in the string, frictional force, Coulomb force etc. Any of these forces can act as a centripetal force.

1. In the case of whirling motion of a stone tied to a string, the centripetal force on the particle is provided by the tensional force on the string. In circular motion in an amusement park, the centripetal force is provided by the tension in the iron ropes.

2. In motion of satellites around the Earth, the centripetal force is given by Earth’s gravitational force on the satellites. Newton’s second law for satellite motion is

Where r- distance of the planet from the centre of the Earth.

Figure 3.39 Whirling motion of objects

$$ m-mass of the satellite $$ $$ v-speed of the satellite $$

3. When a car is moving on a circular track the centripetal force is given by the frictional force between the road and the tyres.

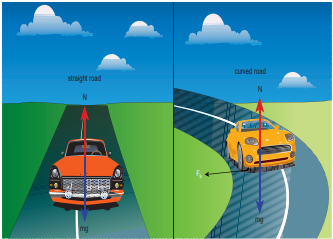
Figure 3.40 Car in the circular track

Newton’s second law for this case is

Even when the car moves on a curved track, the car experiences the centripetal force which is provided by frictional force between the surface and the tyre of the car. This is shown in the Figure 3.41.

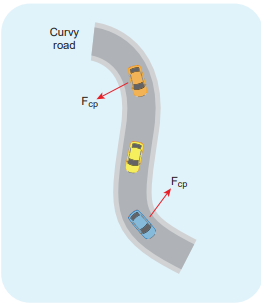
Figure 3.41 Centripetal force due to frictional force between the road and tyre

4. When the planets orbit around the Sun, they experience centripetal force towards the centre of the Sun. Here gravitational force of the Sun acts as centripetal force on the planets as shown in Figure 3.42

Figure 3.42 Centripetal force on the orbiting planet due Sun’s gravity

Newton’s second law for this motion Gravitational force of Sun on the planet = mv r 2

EXAMPLE 3.22

If a stone of mass 0.25 kg tied to a string executes uniform circular motion with a speed of 2 m s-1 of radius 3 m, what is the magnitude of tensional force acting on the stone?

Solution: F cp = mv r 2

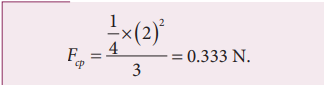
EXAMPLE 3.23

The Moon orbits the Earth once in 27.3 days in an almost circular orbit. Calculate the centripetal acceleration experienced by the Moon? (Radius of the Earth is 6.4 × 106 m)

Solution

The centripetal acceleration is given by a v r = 2 . This expression explicitly depends on Moon’s speed which is non trivial. We can work with the formula

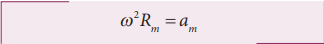
ω is angular velocity.

Rm is the distance between Earth and the Moon, which is 60 times the radius of the Earth.

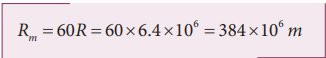
As we know the angular velocity    2 T and T = 27.3 days = 27.3 × 24 × 60 × 60 second = 2.358 × 106 sec

By substituting these values in the formula for acceleration

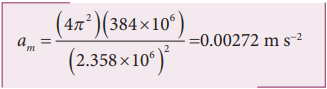
The centripetal acceleration of Moon towards the Earth is 0.00272 m s-2

Note

This result was calculated by Newton himself. In unit 6 we will use this result.

When a vehicle travels in a curved path, there must be a centripetal force acting on it. This centripetal force is provided by the frictional force between tyre and surface of the road. Consider a vehicle of mass ‘m’ moving at a speed ‘v’ in the circular track of radius ‘r’. There are three forces acting on the vehicle when it moves as shown in the Figure 3.43

1. Gravitational force (mg) acting downwards

2. Normal force (N) acting upwards

3. Frictional force (Fs ) acting horizontally inwards along the road

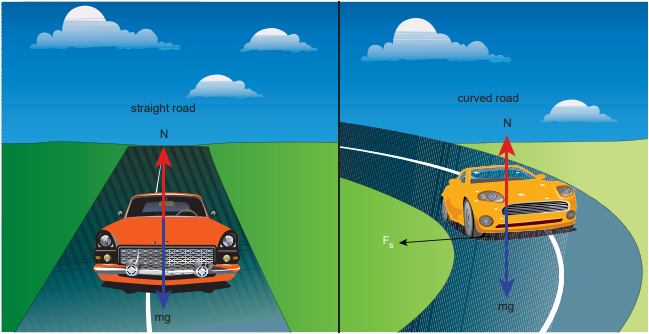
Figure 3.43 Forces acting on the vehicle on a leveled circular road

Suppose the road is horizontal then the normal force and gravitational force are exactly equal and opposite. The centripetal force is provided by the force of static friction Fs between the tyre and surface of the road which acts towards the centre of the circular track,

As we have already seen in the previous section, the static friction can increase from zero to a maximum value

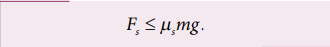
There are two conditions possible:

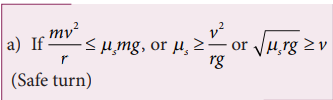
The static friction would be able to provide necessary centripetal force to bend the car on the road. So the coefficient of static friction between the tyre and the surface of the road determines what maximum speed the car can have for safe turn.

If the static friction is not able to provide enough centripetal force to turn, the vehicle will start to skid.

EXAMPLE 3.24

Consider a circular leveled road of radius 10 m having coefficient of static friction 0.81. Three cars (A, B and C) are travelling with speed 7 m s-1 , 8 m s-1 and 10 ms-1 respectively. Which car will skid when it moves in the circular level road? (g =10 m s-2 )

Solution

From the safe turn condition the speed of the vehicle (v) must be less than or equal to s rg

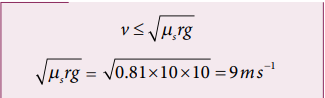
For Car C, v rg s   is less than v

The speed of car A, B and C are 7 m s-1 , 8 m s-1 and 10 m s-1 respectively. The cars A and B will have safe turns. But the car C has speed 10 m s-1 while it turns which exceeds the safe turning speed. Hence, the car C will skid.

In a leveled circular road, skidding mainly depends on the coefficient of static friction ms The coefficient of static friction depends on the nature of the surface which has a maximum limiting value. To avoid this problem, usually the outer edge of the road is slightly raised compared to inner edge as shown in the Figure 3.44. This is called banking of roads or tracks. This introduces an inclination, and the angle is called banking angle.

Figure 3.44 Outer edge of the road is slightly raised to avoid skidding

Let the surface of the road make angle θ with horizontal surface. Then the normal force makes the same angle θ with the vertical. When the car takes a turn, there are two forces acting on the car:

a) Gravitational force mg (downwards)

b) Normal force N (perpendicular to surface)

We can resolve the normal force into two components. N cosθ and N sinθ as shown in Figure 3.46. The component N cosθ balances the downward gravitational force ‘mg’ and component N sinθ will provide the necessary centripetal acceleration. By using Newton second law

The banking angle θ and radius of curvature of the road or track determines the safe speed of the car at the turning. If the speed of car exceeds this safe speed, then it starts to skid outward but frictional force comes into effect and provides an additional centripetal force to prevent the outward skidding. At the same time, if the speed of the car is little lesser than safe speed, it starts to skid inward and frictional force comes into effect, which reduces centripetal force to prevent inward skidding. However if the speed of the vehicle is sufficiently greater than the correct speed, then frictional force cannot stop the car from skidding.

EXAMPLE 3.25

Consider a circular road of radius 20 meter banked at an angle of 15 degree. With what speed a car has to move on the turn so that it will have safe turn?

Solution

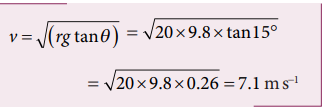
The safe speed for the car on this road is 7.1 m s-1

Circular motion can be analysed from two different frames of reference. One is the inertial frame (which is either at rest or in uniform motion) where Newton’s laws are obeyed. The other is the rotating frame of reference which is a non-inertial frame of reference as it is accelerating. When we examine the circular motion from these frames of reference the situations are entirely different. To use Newton’s first and second laws in the rotational frame of reference, we need to include a pseudo force called ‘centrifugal force’. This ‘centrifugal force’ appears to act on the object with respect to rotating frames. To understand the concept of centrifugal force, we can take a specific case and discuss as done below.

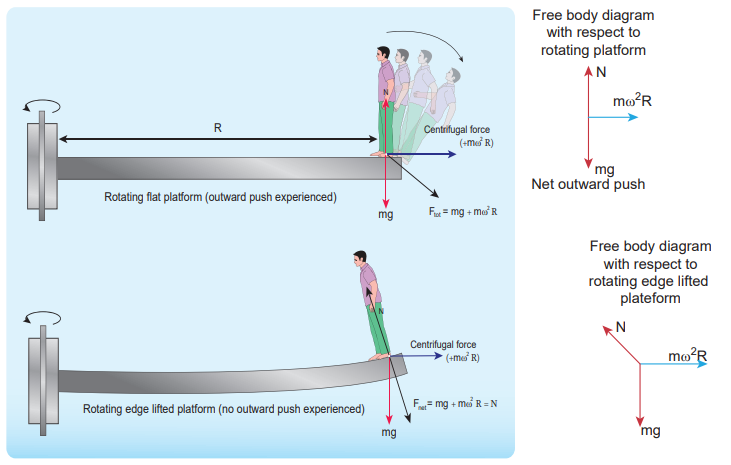
Consider the case of a whirling motion of a stone tied to a string. Assume that the stone has angular velocity ω in the inertial frame (at rest). If the motion of the stone is observed from a frame which is also rotating along with the stone with same angular velocity ω then, the stone appears to be at rest. This implies that in addition to the inward centripetal force m r 2 there must be an equal and opposite force that acts on the stone outward with value +m r 2 . So the total force acting on the stone in a rotating frame is equal to zero (  mrmr   2 2 = 0). This outward force +m r ω2 is called the centrifugal force. The word ‘centrifugal’ means ‘flee from centre’. Note that the ‘centrifugal force’ appears to act on the particle, only when we analyse the motion from a rotating frame. With respect to an inertial frame there is only centripetal force which is given by the tension in the string. For this reason centrifugal force is called as a ‘pseudo force’. A pseudo force has no origin. It arises due to the non inertial nature of the frame considered. When circular motion problems are solved from a rotating frame of reference, while drawing free body diagram of a particle, the centrifugal force should necessarily be included as shown in the Figure 3.45.

Although centrifugal force is a pseudo force, its effects are real. When a car takes a turn in a curved road, person inside the car feels an outward force which pushes the person away. This outward force is also called centrifugal force. If there is sufficient friction between the person and the seat, it will prevent the person from moving outwards. When a car moving in a straight line suddenly takes a turn, the objects not fixed to the car try to continue in linear motion due to their inertia of direction. While observing this motion from an inertial frame, it appears as a straight line as shown in Figure 3.46. But, when it is observed from the rotating frame it appears to move outwards.

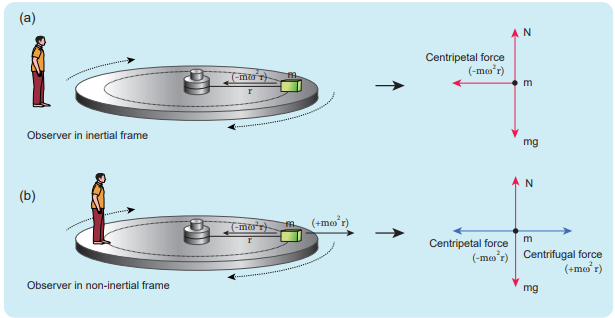
Figure 3.45 Free body diagram of a particle including the centrifugal force

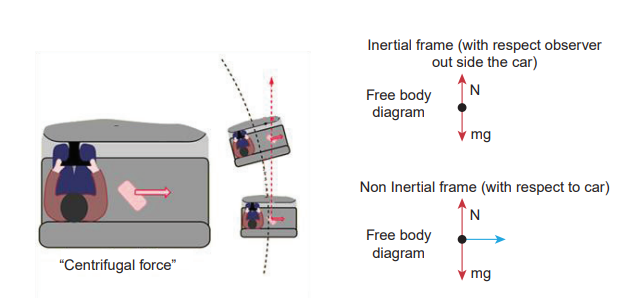
Figure 3.46 Effects of centrifugal force

A person standing on a rotating platform feels an outward centrifugal force and is likely to be pushed away from the platform. Many a time the frictional force between the platform and the person is not sufficient to overcome outward push. To avoid this, usually the outer edge of the platform is little inclined upwards which exerts a normal force on the person which prevents the person from falling as illustrated in Figures 3.47.

Caution!

It is dangerous to stand near the open door (or) steps while travelling in the bus. When the bus takes a sudden turn in a curved road, due to centrifugal force the person is pushed away from the bus. Even though centrifugal force is a pseudo force, its effects are real.

Even though Earth is treated as an inertial frame, it is actually not so. Earth spins about its own axis with an angular velocity ω. Any object on the surface of Earth (rotational frame) experiences a centrifugal force. The centrifugal force appears to act exactly in opposite direction from the axis of rotation. It is shown in the Figure 3.48.

The centrifugal force on a man standing on the surface of the Earth is F m r

where r is perpendicular distance of the man from the axis of rotation. By using right angle triangle as shown in the Figure 3.48, the distance r R= cos θ

Here R = radius of the Earth and   latitude of the Earth where the man is standing.

Figure 3. 48 Centrifugal force acting on a man on the surface of Earth

EXAMPLE 3.26

Calculate the centrifugal force experienced by a man of 60 kg standing at Chennai? (Given: Latitude of Chennai is 13°

Solution The centrifugal force is given by F m c    R 2 cos The angular velocity (ω) of Earth = 2 T  , where T is time period of the Earth (24 hours)

The radius of the Earth R = 6400 Km = 6400 × 103 m

Latitude of Chennai =13°

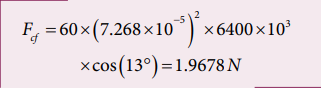
A 60 kg man experiences centrifugal force of approximately 2 Newton. But due to Earth’s gravity a man of 60 kg experiences a force = mg = 60 × 9.8 = 588N. This force is very much larger than the centrifugal force.

Salient features of centripetal and centrifugal forces are compared in Table 3.4.