Decomposition Using Multivalued Dependencies

Some relation schemas, even though they are in BCNF, do not seem to be suffi- ciently normalized, in the sense that they still suffer from the problem of repetition of information. Consider a variation of the university organization where an in- structor may be associated with multiple departments.

inst (ID, dept name, name,street, city)

The astute reader will recognize this schema as a non-BCNF schema because of the functional dependency

ID → name, street, city

and because ID is not a key for inst. Further assume that an instructor may have several addresses (say, a winter

home and a summer home). Then, we no longer wish to enforce the functional dependency “ID→ street, city”, though, of course, we still want to enforce “ID → name” (that is, the university is not dealing with instructors who operate under multiple aliases!). Following the BCNF decomposition algorithm, we obtain two schemas:

r1 (ID, name) r2 (ID, dept name, street, city)

Both of these are in BCNF (recall that an instructor can be associated with multi- ple departments and a department may have several instructors, and therefore, neither “ID → dept name” nor “dept name → ID” hold).

Despite r2 being in BCNF, there is redundancy. We repeat the address informa- tion of each residence of an instructor once for each department with which the instructor is associated. We could solve this problem by decomposing r2 further into:

r21(dept name, ID) r22(ID, street, city)

but there is no constraint that leads us to do this. To deal with this problem, we must define a new form of constraint, called

a multivalued dependency. As we did for functional dependencies, we shall use multivalued dependencies to define a normal form for relation schemas. This normal form, called fourth normal form (4NF), is more restrictive than BCNF. We shall see that every 4NF schema is also in BCNF but there are BCNF schemas that are not in 4NF.

Functional dependencies rule out certain tuples from being in a relation. If A → B, then we cannot have two tuples with the same A value but different B values. Multivalued dependencies, on the other hand, do not rule out the existence of certain tuples. Instead, they require that other tuples of a certain form be present in the relation. For this reason, functional dependencies sometimes are referred to as equality-generating dependencies, and multivalued dependencies are referred to as tuple-generating dependencies.

Let r (R) be a relation schema and let α ⊆ R and β ⊆ R. The multivalued dependency

α →→ β

holds on R if, in any legal instance of relation r (R), for all pairs of tuples t1 and t2 in r such that t1[α] = t2[α], there exist tuples t3 and t4 in r such that

t1[α] = t2[α] = t3[α] = t4[α] t3[β] = t1[β] t3[R − β] = t2[R − β] t4[β] = t2[β] t4[R − β] = t1[R − β]

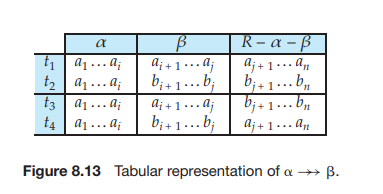
This definition is less complicated than it appears to be. Figure 8.13 gives a tabular picture of t1, t2, t3, and t4. Intuitively, the multivalued dependency α →→ β says that the relationship between α and β is independent of the relationship between α and R−β. If the multivalued dependency α →→ β is satisfied by all relations on schema R, then α →→ β is a trivial multivalued dependency on schema R. Thus, α →→ β is trivial if β ⊆ α or β ∪ α = R.

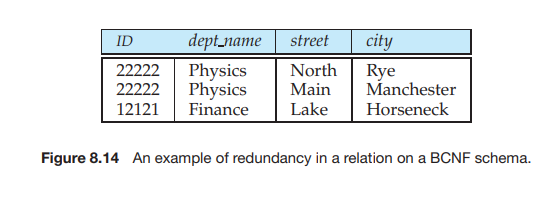
To illustrate the difference between functional and multivalued dependencies, we consider the schema _r_2 again, and an example relation on that schema shown in Figure 8.14. We must repeat the department name once for each address that an instructor has, and we must repeat the address for each department with which an instructor is associated. This repetition is unnecessary, since the relationship between an instructor and his address is independent of the relationship between that instructor and a department. If an instructor with ID 22222 is associated with the Physics department, we want that department to be associated with all of that instructor’s addresses. Thus, the relation of Figure 8.15 is illegal. To make this relation legal, we need to add the tuples (Physics, 22222, Main, Manchester) and (Math, 22222, North, Rye) to the relation of Figure 8.15.

Comparing the preceding example with our definition of multivalued depen- dency, we see that we want the multivalued dependency:

ID →→ street, city

to hold. (The multivalued dependency ID →→ dept name will do as well. We shall soon see that they are equivalent.)

As with functional dependencies, we shall use multivalued dependencies in two ways:

1. To test relations to determine whether they are legal under a given set of functional and multivalued dependencies

2. To specify constraints on the set of legal relations; we shall thus concern ourselves with only those relations that satisfy a given set of functional and multivalued dependencies

Note that, if a relation r fails to satisfy a given multivalued dependency, we can construct a relation r ′ that does satisfy the multivalued dependency by adding tuples to r.

Let D denote a set of functional and multivalued dependencies. The closure D+ of D is the set of all functional and multivalued dependencies logically im- plied by D. As we did for functional dependencies, we can compute D+ from D, using the formal definitions of functional dependencies and multivalued de- pendencies. We can manage with such reasoning for very simple multivalued dependencies. Luckily, multivalued dependencies that occur in practice appear to be quite simple. For complex dependencies, it is better to reason about sets of dependencies by using a system of inference rules.

From the definition of multivalued dependency, we can derive the following rules for α, β ⊆ R:

• If α → β, then α →→ β. In other words, every functional dependency is also a multivalued dependency.

• If α →→ β, then α →→ R − α − β

Appendix C.1.1 outlines a system of inference rules for multivalued dependen- cies.

Consider again our example of the BCNF schema:

r2 (ID, dept name, street, city)

in which the multivalued dependency “ID →→ street, city” holds. We saw in the opening paragraphs of Section 8.6 that, although this schema is in BCNF, the design is not ideal, since we must repeat an instructor’s address information for each department. We shall see that we can use the given multivalued dependency to improve the database design, by decomposing this schema into a fourth normal form decomposition.

A relation schema r (R) is in fourth normal form (4NF) with respect to a set D of functional and multivalued dependencies if, for all multivalued dependencies in D+ of the form α →→ β, where α ⊆ R and β ⊆ R, at least one of the following holds:

• α →→ β is a trivial multivalued dependency.

• α is a superkey for R.

A database design is in 4NF if each member of the set of relation schemas that constitutes the design is in 4NF.

Note that the definition of 4NF differs from the definition of BCNF in only the use of multivalued dependencies. Every 4NF schema is in BCNF. To see this fact, we note that, if a schema r (R) is not in BCNF, then there is a nontrivial functional dependency α → β holding on R, where α is not a superkey. Since α → β implies α →→ β, r (R) cannot be in 4NF.

Let r (R) be a relation schema, and let r1(R1), r2(R2), . . . , rn(Rn) be a decompo- sition of r (R). To check if each relation schema ri in the decomposition is in 4NF, we need to find what multivalued dependencies hold on each ri . Recall that, for a set F of functional dependencies, the restriction Fi of F to Ri is all functional dependencies in F + that include only attributes of Ri . Now consider a set D of both functional and multivalued dependencies. The restriction of D to Ri is the set Di consisting of:

1. All functional dependencies in D+ that include only attributes of Ri .

2. All multivalued dependencies of the form:

α →→ β ∩ Ri

where α ⊆ Ri and α →→ β is in D+.

The analogy between 4NF and BCNF applies to the algorithm for decomposing a schema into 4NF. Figure 8.16 shows the 4NF decomposition algorithm. It is identical to the BCNF decomposition algorithm of Figure 8.11, except that it uses multivalued dependencies and uses the restriction of D+ to Ri .

If we apply the algorithm of Figure 8.16 to (ID, dept name, street, city), we find that _ID_→→ dept name is a nontrivial multivalued dependency, and ID is not a superkey for the schema. Following the algorithm, we replace it by two schemas:

r21 (ID, dept name) r22 (ID, street, city)

This pair of schemas, which is in 4NF, eliminates the redundancy we encountered earlier.

As was the case when we were dealing solely with functional dependencies, we are interested in decompositions that are lossless and that preserve dependen

result := {R};
done := false;
compute D+; Given schema Ri , let Di denote the restriction of D+ to Ri
while (not done) do
if (there is a schema Ri in result that is not in 4NF w.r.t. Di)
then begin
let α →→  be a nontrivial multivalued dependency that holds
on Ri such that  → Ri is not in Di , and α ∩ β = ∅;
result := (result − Ri) ∪ (Ri − β) ∪ (α, β);
end
else done := true;

Figure 8.16 4NF decomposition algorithm.

cies. The following fact about multivalued dependencies and losslessness shows that the algorithm of Figure 8.16 generates only lossless decompositions:

• Let r (R) be a relation schema, and let D be a set of functional and multivalued dependencies on R. Let r1(R1) and r2(R2) form a decomposition of R. This decomposition is lossless of R if and only if at least one of the following multivalued dependencies is in D+:

R1 ∩ R2 →→ R1 R1 ∩ R2 →→ R2

Recall that we stated in Section 8.4.4 that, if R1 ∩ R2 → R1 or R1 ∩ R2 → R2, then r1(R1) and r2(R2) are a lossless decomposition r (R) . The preceding fact about multivalued dependencies is a more general statement about losslessness. It says that, for every lossless decomposition of r (R) into two schemas r1(R1) and r2(R2), one of the two dependencies R1 ∩ R2 →→ R1 or R1 ∩ R2 →→ R2 must hold.

The issue of dependency preservation when we decompose a relation schema becomes more complicated in the presence of multivalued dependencies. Ap- pendix C.1.2 pursues this topic.