Constraints

An E-R enterprise schema may define certain constraints to which the contents of a database must conform. In this section, we examine mapping cardinalities and participation constraints.

Mapping cardinalities, or cardinality ratios, express the number of entities to which another entity can be associated via a relationship set.

Mapping cardinalities are most useful in describing binary relationship sets, although they can contribute to the description of relationship sets that involve more than two entity sets. In this section, we shall concentrate on only binary relationship sets.

For a binary relationship set R between entity sets A and B, the mapping cardinality must be one of the following:

• One-to-one. An entity in A is associated with at most one entity in B, and an entity in B is associated with at most one entity in A. (See Figure 7.5a.)

• One-to-many. An entity in A is associated with any number (zero or more) of entities in B. An entity in B, however, can be associated with at most one entity in A. (See Figure 7.5b.)

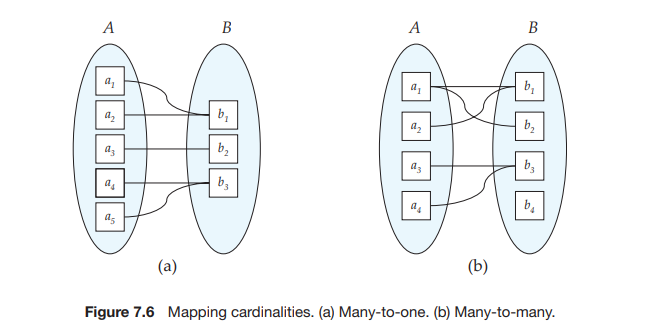
• Many-to-one. An entity in A is associated with at most one entity in B. An entity in B, however, can be associated with any number (zero or more) of entities in A. (See Figure 7.6a.)

• Many-to-many. An entity in A is associated with any number (zero or more) of entities in B, and an entity in B is associated with any number (zero or more) of entities in A. (See Figure 7.6b.)

The appropriate mapping cardinality for a particular relationship set obviously depends on the real-world situation that the relationship set is modeling.

As an illustration, consider the advisor relationship set. If, in a particular university, a student can be advised by only one instructor, and an instructor can advise several students, then the relationship set from instructor to student is one-to-many. If a student can be advised by several instructors (as in the case of students advised jointly), the relationship set is many-to-many.

The participation of an entity set E in a relationship set R is said to be total if every entity in E participates in at least one relationship in R. If only some entities in E participate in relationships in R, the participation of entity set E in relationship R is said to be partial. In Figure 7.5a, the participation of B in the relationship set is total while the participation of A in the relationship set is partial. In Figure 7.5b, the participation of both A and B in the relationship set are total.

For example, we expect every student entity to be related to at least one instructor through the advisor relationship. Therefore the participation of student in the relationship set advisor is total. In contrast, an instructor need not advise any students. Hence, it is possible that only some of the instructor entities are related to the student entity set through the advisor relationship, and the participation of instructor in the advisor relationship set is therefore partial.

We must have a way to specify how entities within a given entity set are distin- guished. Conceptually, individual entities are distinct; from a database perspec- tive, however, the differences among them must be expressed in terms of their attributes.

Therefore, the values of the attribute values of an entity must be such that they can uniquely identify the entity. In other words, no two entities in an entity set are allowed to have exactly the same value for all attributes.

The notion of a key for a relation schema, as defined in Section 2.3, applies directly to entity sets. That is, a key for an entity is a set of attributes that suffice to distinguish entities from each other. The concepts of superkey, candidate key, and primary key are applicable to entity sets just as they are applicable to relation schemas.

Keys also help to identify relationships uniquely, and thus distinguish rela- tionships from each other. Below, we define the corresponding notions of keys for relationships.

The primary key of an entity set allows us to distinguish among the various entities of the set. We need a similar mechanism to distinguish among the various relationships of a relationship set.

Let R be a relationship set involving entity sets E1, E2_, . . . , En_. Let primary- key(Ei ) denote the set of attributes that forms the primary key for entity set Ei . Assume for now that the attribute names of all primary keys are unique. The composition of the primary key for a relationship set depends on the set of attributes associated with the relationship set R.

If the relationship set R has no attributes associated with it, then the set of attributes

primary-key(E~1~) ∪ primary-key(E~2~) ∪···∪ primary-key(E~n~) ∪ {a~1~, a~2~,…, a~m~}

describes an individual relationship in set R. If the relationship set R has attributes a1,a2, . . . , am_ associated with it, then the set of attributes

primary-key(E_1) ∪ primary-key(E_2) ∪ · · · ∪ primary-key(En) ∪ {a_1, a_2, . . . , am}

describes an individual relationship in set R. In both of the above cases, the set of attributes

primary-key(E~1~) ∪ primary-key(E~2~) ∪···∪ primary-key(E~n~)

forms a superkey for the relationship set. If the attribute names of primary keys are not unique across entity sets, the

attributes are renamed to distinguish them; the name of the entity set combined with the name of the attribute would form a unique name. If an entity set par- ticipates more than once in a relationship set (as in the prereq relationship in Section 7.2.2), the role name is used instead of the name of the entity set, to form a unique attribute name.

The structure of the primary key for the relationship set depends on the mapping cardinality of the relationship set. As an illustration, consider the entity sets instructor and student, and the relationship set advisor, with attribute date, in Section 7.2.2. Suppose that the relationship set is many-to-many. Then the primary key of advisor consists of the union of the primary keys of instructor and student. If the relationship is many-to-one from student to instructor—that is, each student can have have at most one advisor—then the primary key of advisor is simply the primary key of student. However, if an instructor can advise only one student— that is, if the advisor relationship is many-to-one from instructor to student—then the primary key of advisor is simply the primary key of instructor. For one-to-one relationships either candidate key can be used as the primary key.

For nonbinary relationships, if no cardinality constraints are present then the superkey formed as described earlier in this section is the only candidate key, and it is chosen as the primary key. The choice of the primary key is more complicated if cardinality constraints are present. Since we have not discussed how to specify cardinality constraints on nonbinary relations, we do not discuss this issue further in this chapter. We consider the issue in more detail later, in Sections 7.5.5 and 8.4.