Classic Problems of Synchronization
In this section, we present a number of synchronization problems as examples of a large class of concurrency-control problems. These problems are used for testing nearly every newly proposed synchronization scheme. In our solutions to the problems, we use semaphores for synchronization, since that is the
while (true) { . . .
/* produce an item in next produced */ . . .
wait(empty); wait(mutex);
. . .*/ *add next produced to the buffer */
. . . signal(mutex); signal(full);
}
Figure 7.1 The structure of the producer process.
traditional way to present such solutions. However, actual implementations of these solutions could use mutex locks in place of binary semaphores.
The Bounded-Buffer Problem
The **bounded-buffer problem**was introduced in Section 6.1; it is commonly used to illustrate the power of synchronization primitives. Here, we present a gen- eral structure of this scheme without committing ourselves to any particular implementation. We provide a related programming project in the exercises at the end of the chapter.
In our problem, the producer and consumer processes share the following data structures:
int n; semaphore mutex = 1;
semaphore empty = n;
semaphore full = 0
We assume that the pool consists of n buffers, each capable of holding one item. The mutex binary semaphore provides mutual exclusion for accesses to the buffer pool and is initialized to the value 1. The empty and full semaphores count the number of empty and full buffers. The semaphore empty is initialized to the value n; the semaphore full is initialized to the value 0.
The code for the producer process is shown in Figure 7.1, and the code for the consumer process is shown in Figure 7.2. Note the symmetry between the producer and the consumer. We can interpret this code as the producer producing full buffers for the consumer or as the consumer producing empty buffers for the producer.
The Readers–Writers Problem
Suppose that a database is to be shared among several concurrent processes. Some of these processes may want only to read the database, whereas others may want to update (that is, read and write) the database. We distinguish
while (true) { wait(full); wait(mutex);
. . .*/ *remove an item from buffer to next consumed */
. . . signal(mutex); signal(empty);
. . .*/ *consume the item in next consumed */
. . . }
Figure 7.2 The structure of the consumer process.
between these two types of processes by referring to the former as readers and to the latter as writers. Obviously, if two readers access the shared data simultaneously, no adverse effects will result. However, if a writer and some other process (either a reader or a writer) access the database simultaneously, chaos may ensue.
To ensure that these difficulties do not arise, we require that the writers have exclusive access to the shared databasewhilewriting to the database. This synchronization problem is referred to as the readers–writers problem. Since it was originally stated, it has been used to test nearly every new synchronization primitive.
The readers–writers problem has several variations, all involving priori- ties. The simplest one, referred to as the first readers–writers problem, requires that no reader be kept waiting unless a writer has already obtained permission to use the shared object. In other words, no reader should wait for other read- ers to finish simply because a writer is waiting. The second readers–writers problem requires that, once a writer is ready, that writer perform its write as soon as possible. In other words, if a writer is waiting to access the object, no new readers may start reading.
A solution to either problem may result in starvation. In the first case, writers may starve; in the second case, readers may starve. For this reason, other variants of the problem have been proposed. Next, we present a solution to the first readers–writers problem. See the bibliographical notes at the end of the chapter for references describing starvation-free solutions to the second readers–writers problem.
In the solution to the first readers–writers problem, the reader processes share the following data structures:
semaphore rw mutex = 1; semaphore mutex = 1; int read count = 0;
The binary semaphores mutex and rw mutex are initialized to 1; read count is a counting semaphore initialized to 0. The semaphore rw mutex
while (true) { wait(rw mutex);
. . .*/ *writing is performed */
. . . signal(rw mutex);
}
Figure 7.3 The structure of a writer process.
is common to both reader and writer processes. The mutex semaphore is used to ensure mutual exclusion when the variable read count is updated. The read count variable keeps track of how many processes are currently reading the object. The semaphore rw mutex functions as a mutual exclusion semaphore for the writers. It is also used by the first or last reader that enters or exits the critical section. It is not used by readers that enter or exit while other readers are in their critical sections.
The code for a writer process is shown in Figure 7.3; the code for a reader process is shown in Figure 7.4. Note that, if a writer is in the critical section and n readers are waiting, then one reader is queued on rw mutex, and n − 1 readers are queued on mutex. Also observe that, when a writer executes sig- nal(rw mutex), we may resume the execution of either the waiting readers or a single waiting writer. The selection is made by the scheduler.
The readers–writers problem and its solutions have been generalized to provide reader–writer locks on some systems. Acquiring a reader–writer lock requires specifying the mode of the lock: either read or write access. When a
while (true) { wait(mutex); read count++; if (read count == 1)
wait(rw mutex); signal(mutex);
. . .*/ *reading is performed */
. . . wait(mutex); read count--; if (read count == 0)
signal(rw mutex); signal(mutex);
}
Figure 7.4 The structure of a reader process.
process wishes only to read shared data, it requests the reader–writer lock in read mode. A process wishing to modify the shared data must request the lock in write mode. Multiple processes are permitted to concurrently acquire a reader–writer lock in read mode, but only one process may acquire the lock for writing, as exclusive access is required for writers.
Reader–writer locks are most useful in the following situations:
• In applications where it is easy to identify which processes only read shared data and which processes only write shared data.
• In applications that have more readers than writers. This is because reader–writer locks generally require more overhead to establish than semaphores or mutual-exclusion locks. The increased concurrency of allowing multiple readers compensates for the overhead involved in setting up the reader–writer lock.
The Dining-Philosophers Problem
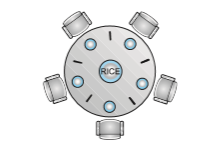
Consider five philosophers who spend their lives thinking and eating. The philosophers share a circular table surrounded by five chairs, each belonging to one philosopher. In the center of the table is a bowl of rice, and the table is laid with five single chopsticks (Figure 7.5). When a philosopher thinks, she does not interact with her colleagues. From time to time, a philosopher gets hungry and tries to pick up the two chopsticks that are closest to her (the chopsticks that are between her and her left and right neighbors). Aphilosopher may pick up only one chopstick at a time. Obviously, she cannot pick up a chopstick that is already in the hand of a neighbor. When a hungry philosopher has both her chopsticks at the same time, she eats without releasing the chopsticks. When she is finished eating, she puts down both chopsticks and starts thinking again.
The dining-philosophers problem is considered a classic synchronization problem neither because of its practical importance nor because computer scientists dislike philosophers but because it is an example of a large class of concurrency-control problems. It is a simple representation of the need
while (true) { wait(chopstick[i]); wait(chopstick[(i+1) % 5]);
. . .*/ *eat for a while */
. . . signal(chopstick[i]); signal(chopstick[(i+1) % 5]);
. . .*/ *think for awhile */
. . . }
Figure 7.6 The structure of philosopher i.
to allocate several resources among several processes in a deadlock-free and starvation-free manner.
Semaphore Solution
One simple solution is to represent each chopstick with a semaphore. A philosopher tries to grab a chopstick by executing a wait() operation on that semaphore. She releases her chopsticks by executing the signal() operation on the appropriate semaphores. Thus, the shared data are
semaphore chopstick[5];
where all the elements of chopstick are initialized to 1. The structure of philosopher i is shown in Figure 7.6.
Although this solution guarantees that no two neighbors are eating simul- taneously, it nevertheless must be rejected because it could create a deadlock. Suppose that all five philosophers become hungry at the same time and each grabs her left chopstick. All the elements of chopstick will now be equal to 0. When each philosopher tries to grab her right chopstick, she will be delayed forever.
Several possible remedies to the deadlock problem are the following:
• Allow at most four philosophers to be sitting simultaneously at the table.
• Allow a philosopher to pick up her chopsticks only if both chopsticks are available (to do this, she must pick them up in a critical section).
• Use an asymmetric solution—that is, an odd-numbered philosopher picks up first her left chopstick and then her right chopstick, whereas an even- numbered philosopher picks up her right chopstick and then her left chopstick.
In Section 6.7, we present a solution to the dining-philosophers problem that ensures freedom from deadlocks. Note, however, that any satisfactory solution to the dining-philosophers problemmust guard against the possibility that one of the philosophers will starve to death. Adeadlock-free solution does not necessarily eliminate the possibility of starvation.
Monitor Solution
Next, we illustrate monitor concepts by presenting a deadlock-free solution to the dining-philosophers problem. This solution imposes the restriction that a philosopher may pick up her chopsticks only if both of them are available. To code this solution, we need to distinguish among three states in which wemay find a philosopher. For this purpose,we introduce the following data structure:
enum {THINKING, HUNGRY, EATING} state[5];
Philosopher _i_ can set the variable state[i] = EATING only if her two neigh- bors are not eating: (state[(i+4) % 5] != EATING) and (state[(i+1) % 5] != EATING).
We also need to declare
condition self[5];
This allows philosopher i to delay herself when she is hungry but is unable to obtain the chopsticks she needs.
We are now in a position to describe our solution to the dining- philosophers problem. The distribution of the chopsticks is controlled by the monitor DiningPhilosophers, whose definition is shown in Figure 7.7. Each philosopher, before starting to eat, must invoke the operation pickup(). This act may result in the suspension of the philosopher process. After the successful completion of the operation, the philosopher may eat. Following this, the philosopher invokes the putdown() operation. Thus, philosopher i must invoke the operations pickup() and putdown() in the following sequence:
DiningPhilosophers.pickup(i); ... eat ...
DiningPhilosophers.putdown(i);
It is easy to show that this solution ensures that no two neighbors are eating simultaneously and that no deadlocks will occur. As we already noted, however, it is possible for a philosopher to starve to death. We do not present a solution to this problem but rather leave it as an exercise for you.