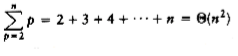One of the simplest sorting algorithms is the insertion sort. Insertion sort consists of n - 1 passes. For pass p = 2 through n, insertion sort ensures that the elements in positions 1 through p are in sorted order. Insertion sort makes use of the fact that elements in positions 1 through p - 1 are already known to be in sorted order. figure 7.1 shows a sample file after each pass of insertion sort.

figure 7.1 shows the general strategy. In pass p, we move the pth element left until its correct place is found among the first p elements. The code in figure 7.2 implements this strategy. The sentinel in a[0] terminates the while loop in the event that in some pass an element is moved all the way to the front. Lines 3 through 6 implement that data movement without the explicit use of swaps. The element in position p is saved in tmp, and all larger elements (prior to position p) are moved one spot to the right. Then tmp is placed in the correct spot. This is the same technique that was used in the implementation of binary heaps.

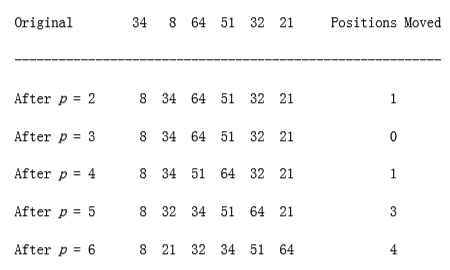
void insertion_sort(input_type a[], unsigned int n){

unsigned int j, p;

input_type tmp;

/*1*/ a[0] = MIN_DATA; /* sentinel */

/*2*/ for(p=2; p <= n; p++)
{

/*3*/ tmp = a[p];

/*4*/ for(j = p; tmp < a[j-1]; j--)

/*5*/ a[j] = a[j-1];


/*6*/ a[j] = tmp;

}

}

figure 7.2 Insertion sort routine.

Because of the nested loops, each of which can take n iterations, insertion sort

is O(n2). Furthermore, this bound is tight, because input in reverse order can actually achieve this bound. A precise calculation shows that the test at line 4 can be executed at most p times for each value of p. Summing over all p gives a total of