Binary heaps are so simple that they are almost always used when priority queues are needed. A simple generalization is a d-heap, which is exactly like a binary heap except that all nodes have d children (thus, a binary heap is a 2-heap). Figure 6.19 shows a 3-heap.

Notice that a d-heap is much more shallow than a binary heap, improving the running time of inserts to O(logdn). However, the delete_min operation is more expensive, because even though the tree is shallower, the minimum of d children must be found, which takes d - 1 comparisons using a standard algorithm. This raises the time for this operation to O(d logdn). If d is a constant, both running times are, of course, O(log n). Furthermore, although an array can still be used, the multiplications and divisions to find children and parents are now by d, which seriously increases the running time, because we can no longer implement division by a bit shift. d-heaps are interesting in theory, because there are many algorithms where the number of insertions is much greater than the number of delete_mins (and thus a theoretical speedup is possible). They are also of interest when the priority queue is too large to fit entirely in main memory. In this case, a d-heap can be advantageous in much the same way as B-trees.

The most glaring weakness of the heap implementation, aside from the inability to perform finds is that combining two heaps into one is a hard operation. This extra operation is known as a merge. There are quite a few ways of implementing heaps so that the running time of a merge is O(log n). We will now discuss three data structures, of various complexity, that support the merge operation efficiently. We will defer any complicated analysis until Chapter 11.

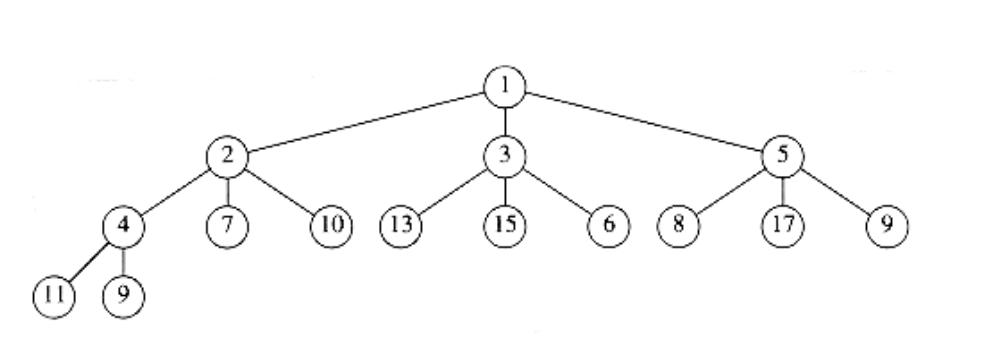
Figure 6.19 A d-heap